Dans ce qui suit, on ne considérera que l'aimantation résultant de la somme (vectorielle) de tous les moments magnétiques associés aux spins nucléaires ou électroniques.

Cette magnétisation est initialement M0, le long de Oz. On a vu qu'à la résonance (c'est à dire pour w=w₀), le champ effectif est en fait le champ B1 tournant, qui est le long de Ox' dans le repère tournant. A partir de maintenant, on ne se placera que dans le repère tournant que l'on dénommera Oxyz (en oubliant les "primes")

Impulsion

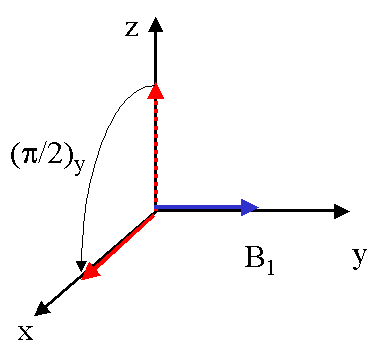
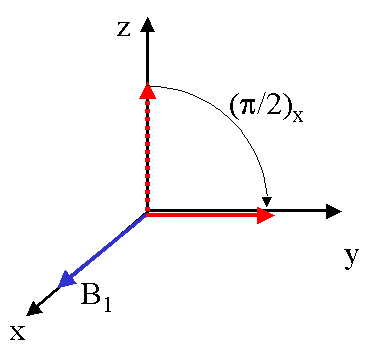
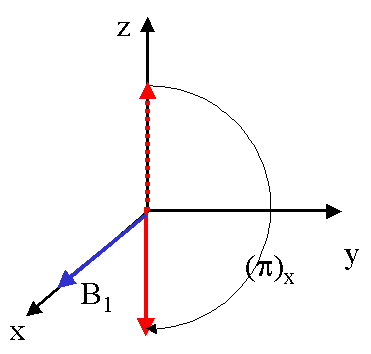
Si on envoie sur l'échantillon une impulsion pendant une durée ti, celle-ci fera donc tourner l'aimantation M₀ autour de B₁, avec une précession de fréquence w1 = - g.B₁. l'angle parcouru par M₀ sera donc q=w₁.t_i. En choisissant convenablement B₁ et t_i, il est donc aisé de provoquer la rotation de M₀ d'angles prévus à l'avance : on parlera alors des plus courantes, qui amènent M₀ sur l'axe Oy et Oz (valeurs négatives) respectivement.
d'impulsions

de p/2
ou de p
En jouant sur la phase de l'impulsion, la même opération peut se faire autour de Oy plutôt que de Ox.

L'impulsion de pulsation w₀ dure un temps court. De ce fait, elle contient une certaine imprécision sur la fréquence envoyée, comme indiqué dans la partie traitant de la transformation de Fourier.
 

Relaxation, précession libre (FID) et spectre

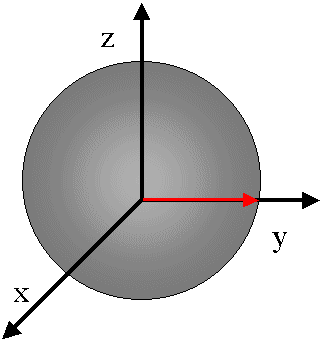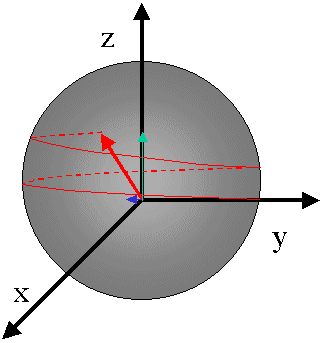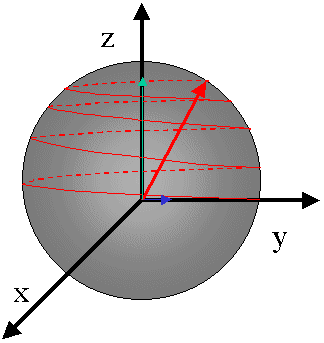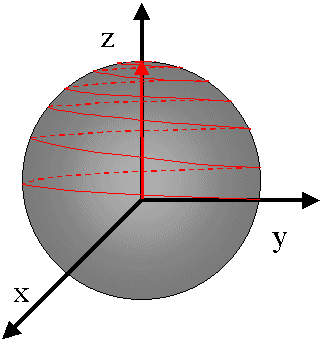
A la fin de l'impulsion, l'aimantation atteint sa nouvelle position (sur Oy, à la suite d'une impulsion  (p/2)_xpar exemple). Bien entendu, elle ne peut s'y maintenir et elle tendra à rejoindre sa position initiale, le long de Oz. Pour cela, l'aimantation tournera autour de B₀, avec sa fréquence w₀= g.B₀ (pas forcément identique à la valeur de w qui sert à la mesure du signal: différents noyaux résonnent à différentes fréquences). Pendant le même temps sa composante sur Oy deviendra nulle, avec un temps caractéristique T₂.

 

	La composante selon Oy, c'est à dire le signal observé, est donc composé d'un  signal périodique diminuant jusqu'à une valeur nulle selon l'expression suivante : My = e-t/T2.cos (w-w0)t
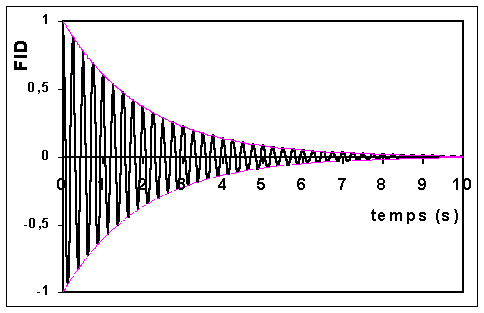
Le signal a donc la forme ci-contre en fonction du temps. Il disparaît avec la constante de temps T2, qui est de l'ordre de la seconde. Le signal  est ici obtenu pour n= 4Hz et T2=2s. Comme discuté plus loin, la transformée de Fourier de ce signal est une fonction de  la fréquence (inverse du temps). Il est appelé signal de précession libre ou  FID (free induction decay). Il donne le spectre lui-même. l'énorme avantage de cette méthode de RMN à impulsion est que les spectre est donc obtenu après un  temps de l'ordre de la seconde. On peut donc accumuler un grand nombre de FID et  ainsi améliorer grandement le rapport signal/bruit, c'est à dire la qualité  du spectre. Le temps de calcul de la transformée de Fourier qui se fait après accumulation est négligeable car on dispose d'algorithmes rapides pour ce type  de calcul.
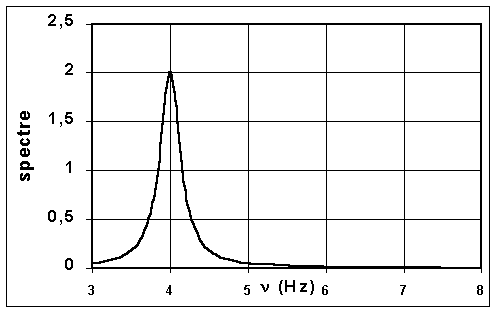
	Le spectre correspondant au FID ci-dessus est donné ci-contre. Il est donc constitué d'une seule raie de largeur à mi-hauteur d'environ 0,3 Hz.

Echo de spin

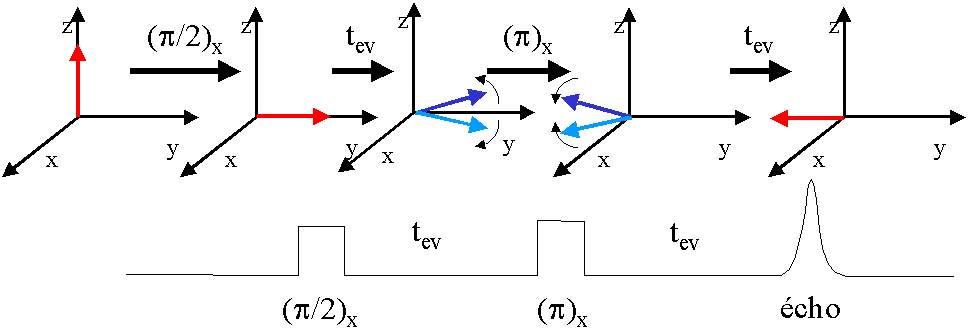
Il s'agit d'une technique de re focalisation de l'aimantation provenant de plusieurs noyaux (fréquences différentes) particulièrement utile pour l'imagerie par RMN. Deux impulsions sont utilisées l'une après l'autre, séparées par un intervalle de temps connu. Une première impulsion  (p/2)_x bascule l'aimantation sur Oy. Les noyaux différents vont alors précesser autour de B₀ avec leur fréquence propre, de telle façon qu'ils se distribuent autour de Oy, certains en retard d'autres en avance. Le dessin ci-dessous représente ce qui se passe pour 2 noyaux différents.

 

Après un temps t_ev, on envoie une impulsion (p)_x. Elle bascule les deux aimantations autour de -Oy, chacune gardant son sens de progression dans le référentiel tournant. Elles vont donc s'additionner de nouveau sur -Oy après un nouvel intervalle de temps t_evpostérieur à la deuxième impulsion. Ceci produit alors un signal en écho facile à mesurer puisqu'il rassemble tous les noyaux de l'échantillon.