Expérimentalement, on observe des modifications très nettes du spectre de RMN qui amènent à introduire cette notion importante.
 

Inéquivalence chimique de noyaux apparement équivalents

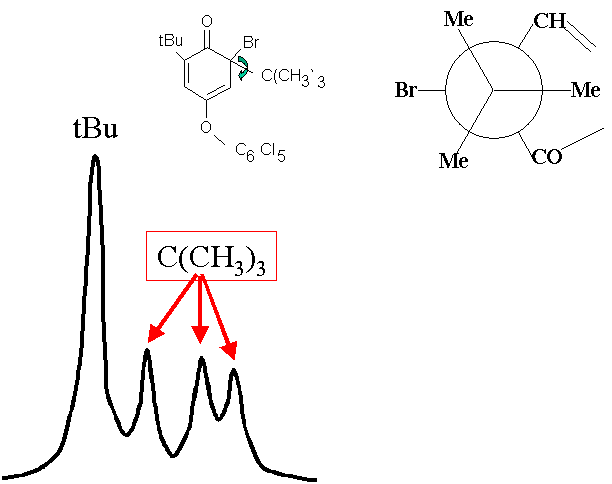
Dans la figure ci-dessous (spectre de RMN ¹H), on voit que les 3 méthyles de l'un des tBu (appelé tBu1, celui qui est sur le carbone qui porte l'atome de brome) ne sont pas équivalents chimiquement, puisqu'ils présentent chacun une raie. Par contre, ceux du tBu2 qui se trouve sur la face gauche de la molécule ne donne qu'une raie. Comme le montre la représentation de Newman de la liaison entre les 3 méthyles de tBu1 et l'atome de carbone qui les porte, les 3 méthyles n'ont pas un environnement identique. La différence entre les deux tBu est que le premier à un environnement immédiat trop encombré pour qu'il puisse tourner vite, tandis que l'autre est beaucoup plus libre de ses mouvements.

 

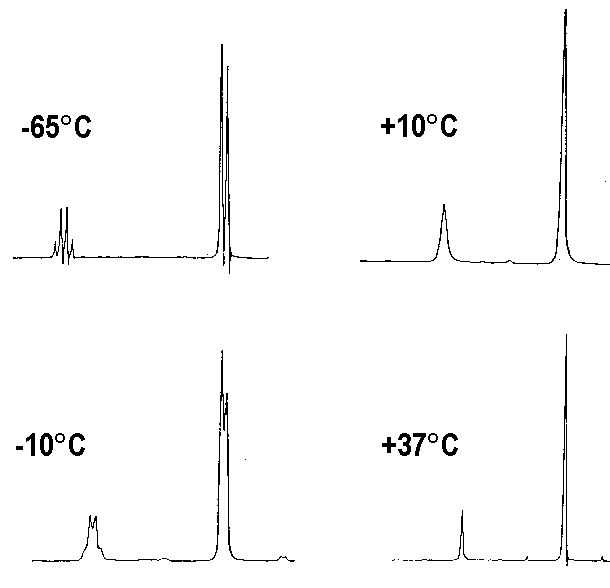
Un autre exemple de spectre de ¹H est celui du méthanol (CH^a₃OH^b) qui manifeste un couplage entre le proton b et les protons a seulement à basse température. On interprète ce fait par un échange rapide de H^b entre toutes les molécules de méthanol seulement à température supérieure à 10°C * environ. En dessous de cette température, chaque proton H^b reste un temps suffisamment long sur une molécule donnée pour que le couplage se manifeste.

 

Mais que signifie échange lent ou rapide? Pour le comprendre il faut introduire cet échange dans les équations de Bloch et voir ce que cela change.

 

Analyse quantitative de l'échange

On reprend les 3 équations de Bloch démontrées dans le chapitre précédent.

(dM/dt)_x'M_y' = (w-w₀) - M_x'/T₂  = 0

(dM/dt)_y'= -M_x' (w-w₀) + g.M_z.B₁ - M_y'/T₂ = 0

(dM /dt)_z'= - g.M_y' B₁ + (M₀-M_z)/T₁ = 0

On écrit d'abord la magnétisation du proton considéré dans les 2 environnements A et B inéquivalents chimiquement par 6 équations (2 x 3). On exprime ensuite (termes en rouge) que la magnétisation des protons A décroit avec un temps caractéristique t_A (temps de vie du proton dans le site A), mais augmente par l'apport de la magnétisation des protons qui viennent du site B, avec un temps caractéristique t_B (temps de vie du proton dans le site B).

(dM^A / dt)_x' = (w-w^A₀) - M^A_x' /T ^A₂  - M^A_x' / t^A + M^B_x' / t^B= 0

(dM^A / dt)_y'= -M^A_x' (w-w^A₀) + g.M^A_z.B₁ - M^A_y'/T₂ - M^A_y' / t^A + M^B_y' / t^B= 0

(dM^A / dt)_z'= - g.M^A_y' B₁ + (M^A₀-M^A_z) / T₁- M^A_z' / t^A + M^B_z' / t^B = 0

(dM^B / dt)_x' = (w-w^B₀) - M^B_x' /T ^B₂  - M^B_x' / t^B + M^A_x' / t^A= 0

(dM^B / dt)_y'= -M^B_x' (w-w^B₀) + g.M^B_z.B₁ - M^B_y'/T₂- M^B_y' / t^B + M^A_y' / t^A= 0

(dM^B / dt)_z'= - g.M^B_y' B₁ + (M^B₀-M^B_z) / T₁- M^B_z' / t^B + M^A_z' / t^A = 0

Puisque le principe du quasi équilibre s'applique encore, tout se ramène à un système de 6 équations à 6 inconnues (les magnétisations). Le signal expérimental est la somme des magnétisations sur y'. Le calcul se fait très bien sur un ordinateur. Il donne les résultats ci-dessous.
 

Prévisions de spectres en situation d'échange

• Deux sites A et B, peuplés également: premier exemple
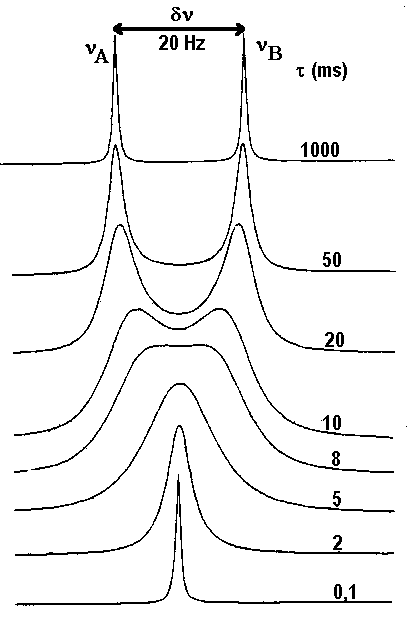
  Le calcul fait pour deux fréquences de résonances distantes de 20Hz donne  le résultat ci-dessous :
  
   
•  

On voit que l'on passe progressivement de deux raies lorsque la durée de vie dans chaque site (qui et la même, puisque les sites sont également peuplés) est longue (1s) à une raie unique quand t devient très court ( inférieur à 8 ms environ). Le spectre passe pour t=  8 ms par un état qualifié de "coalescence" où les deux pics ne se distinguent plus. On peut démontrer que le temps de vie à la coalescence est donné par t_coal.= 1/2pDn.  C'est donc le t_coal. qui sert de référence pour distinguer les échanges rapides (t<t_coal.)  des échanges lents (t>t _coal.). Dans cet exemple, t_coal. = 1/2pDn = 8s. Enfin, le pic unique ( pour l'échange  rapide) est situé juste à égale distance des pics individuels (obtenus dans  la situation de l'échange lent).

Deux sites A et B, peuplés également: deuxième exemple
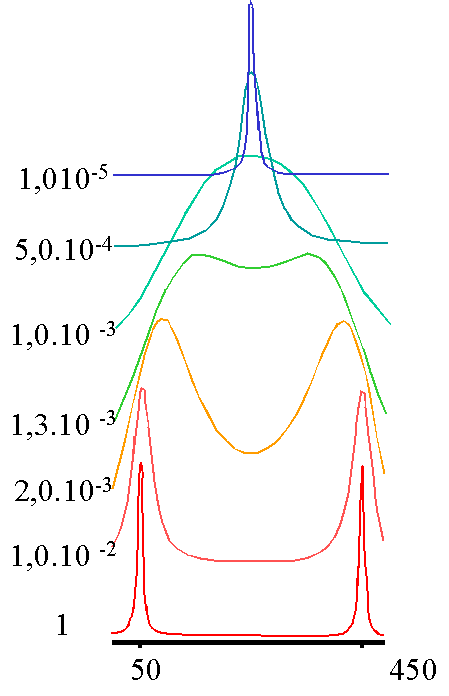
Si la différence de fréquence est beaucoup plus grande (400Hz), l'allure générale  des spectres est la même, mais avec une échelle de temps différente. On voit que la coalescence apparaît pour un temps de vie de l'ordre de 4.10^-4s, en accord avec l'expression indiquée ci-dessus.

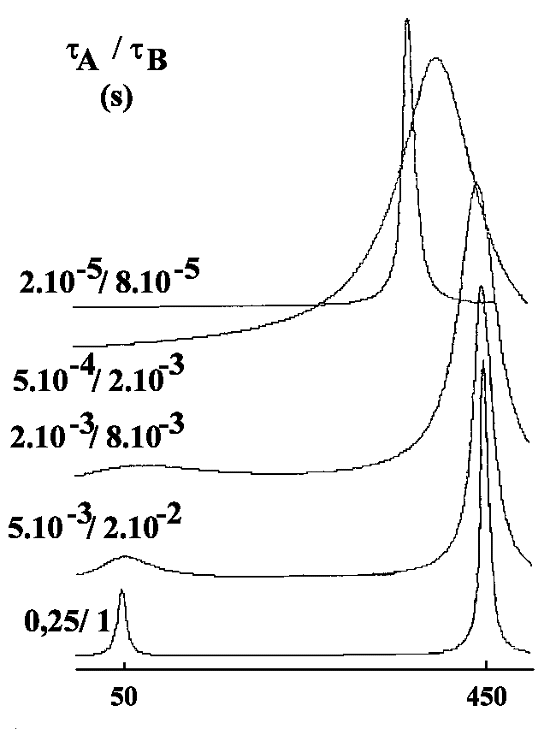
Deux sites A et B, peuplés inégalement

Le résultat du calcul est donné ci-dessous pour 2 exemples différents :

 

1. t_A / t_B=  4 : le site A est occupé 4 fois plus longtemps que le site B. La population du site A est donc p_A =t_A / (t_A + t_B)  = 4 / 5. Pour la même raison p_B = t_B / (t_A + t_B)  = 1 / 5 (avec évidemment p_A + p_B =1.
   
    
2.  

Pour un échange lent, les deux pics individuels sont dans le rapport de  leur population (soit 4). Quand les temps de vie diminuent, le phénomène de coalescence se manifeste également. Enfin, pour les durées de vie les  plus courtes, un seul pic apparaît (d'intensité 5). Dans l'exemple ci-dessus  où Dn= 400 Hz, le pic unique se situe à la  fréquence 370 Hz. On peut démontrer que cette fréquence correspond à
n_exp = p_A.n_A + p_B.n_B,
c'est à dire à la moyenne pondérée des deux fréquences n_A et n_B. Cette relation est générale  comme on va le voir ci-dessous.

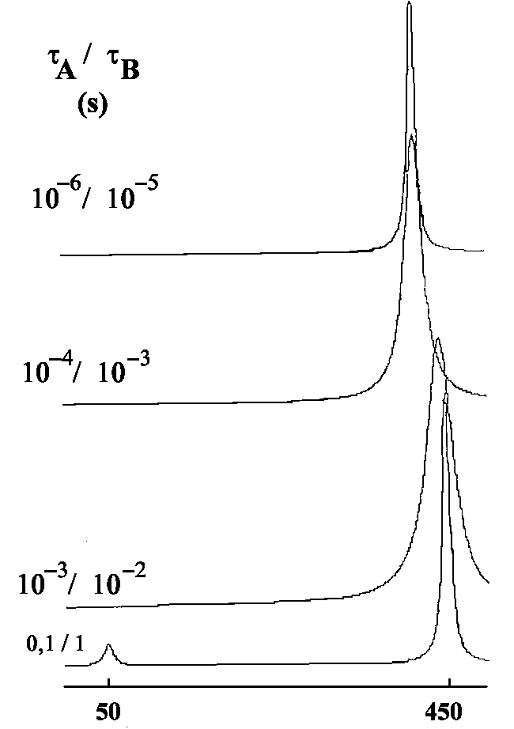
t_A / t_B=  10: le site A est occupé 10 fois plus longtemps que le site B. La  population du site A est donc p_A =t_A / (t_A + t_B)  = 10 / 11. Pour la même raison p_B = t_B / (t_A + t_B)  = 1 / 11 (avec toujours p_A + p_B =1.

Pour un échange lent, les deux pics individuels sont dans le rapport de  leur population (soit 10). Quand les temps de vie diminuent, le phénomène de coalescence se manifeste encore. Enfin, pour les durées de vie les  plus courtes, un seul pic apparaît (d'intensité 11). Dans l'exemple ci-dessus où Dn= 400 Hz, le pic unique se situe à la  fréquence ~420 Hz, toujours donnée par la même relation.
n_exp = p_A.n_A + p_B.n_B,


Systèmes à plus de deux sites

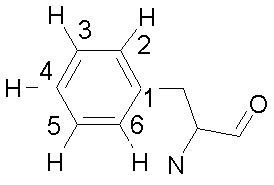
La théorie est du même type que déjà vu, avec simplement un nombre d'équations linéaires plus grand (3 fois le nombre de sites). La figure ci-dessous montre un exemple de résultat de calcul avec un cycle benzénique d'une phényl alanine

 

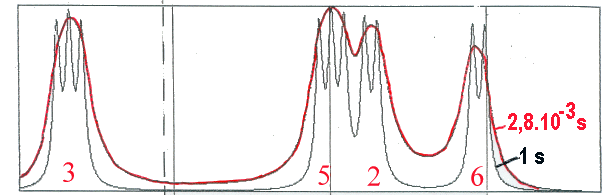
qui s'échange entre deux positions dans une protéine. Les protons 2, 3, 5  et 6 (le proton 4 se situant dans une autre région du spectre) ne sont pas  équivalents dans chacune des positions du cycle. Ils sont donc couplés avec  leurs plus proches voisins. L'échange se fait entre deux populations égales (puisque le cycle est symétrique) avec 2 temps de vie différents (d'autres sont présentés dans un autre lieu) à titre d'exemple.