Point de départ

Ici, nous ne ferons qu'un description des principes fondamentaux qui permettent de comprendre les articles où la Résonance magnétique (RM), nucléaire (RMN) ou électronique (RPE) est utilisée en Biologie. Les fondements physiques du magnétisme nucléaire ne sont pas abordés, de même que la description quantique du phénomène de résonance. Dans tout ce qui suit les vecteursseront représentés par des caractères gras, et les scalaires par des caractères ordinaires.
De nombreux sites apportent des développements utiles (et souvent beaucoup plus approfondis que le présent site qui est destiné à des biochimistes). Les plus intéressants sont les deux sites indiqués ci-dessus.
On admettra l'existence d'un moment magnétique (nucléaire ou électronique) qui a un certain nombre de propriétés (cf tableau de valeurs) qui dépendent du noyau ou électron considéré :

• un spin I, qui ne peut prendre que des valeurs entières et demi entières.
• un moment magnétique µ (dit de spin) définit comme suit :
• une projection sur un axe z µ_z = hg/2p.m_I, où g est le facteur gyromagnétique. On le nomme ainsi par référence à l'expression du moment magnétique orbital de l'électron qui tournerait sur un cercle. Cette grandeur (mécanique) L= m_e.v.rqui est associé à un moment magnétique µ= - g.L (en fait, le moment orbital est quantifié, mais la relation µ= - g.L persiste).  La valeur de g est différente pour les différentes particules (cf tableau)
• un module ½µ½=hg/2p[I(I+1]^1/2 où m_I prend les valeurs -I, -I+1, -I+2 ...I-2, I-1, I (par exemple, pour I=1/2, m_I= -1/2 et +1/2)

Orientation et mouvement d'un moment magnétique isolé situé dans un champ magnétique.

Selon les expressions ci-dessus, considérons deux exemples :

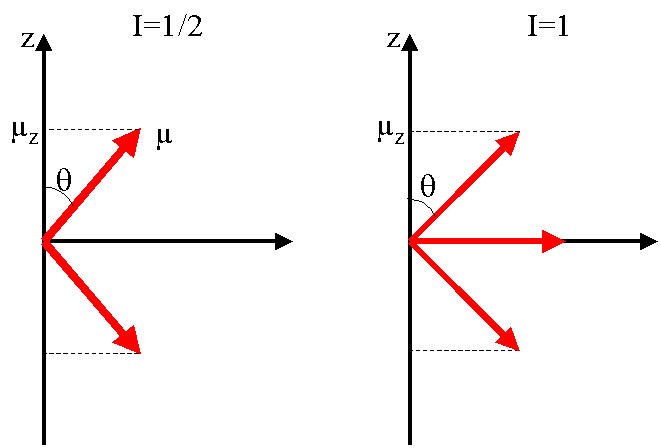
• I=1/2: alors µ_z = ±1/2.hg/2p et ½µ½=hg/2p .Ö3/2 . Cela impose un angle q entre µ et l'axe Oz tel que Arccos(q)=Ö3/3 soit q= 54°73.
• I=1: alors µ_z=±hg/2pet 0 tandis que ½µ½=hg/2p .Ö2. Cela impose un angle q entre µ et l'axe Oz tel que Arccos(q)=Ö2/2 soit q= 45°.

Sur l'exemple d'un noyau de spin 1/2, la figure ci-dessus montre la disposition des moments magnétiques auxquels correspondent les valeurs de µ_z. Chacun peut occuper toutes les positions possibles sur le tronc de cône sur lequel la valeur de µ_z le fixe.   Les composantes de µ sur les trois axes sont données pour une position. Mais à cause du champ magnétique B₀, axé sur Oz, le moment magnétique est soumis à un mouvement circulaire uniforme.

le champ B₀ produit un couple Gsur µ: par définition  G= µx B₀où x représente le produit vectoriel. Ce couple provoque le déplacement du moment angulaire, selon la Loi de Newton: dL/dt =G . En tenant compte de la relation µ=   g.Lon trouve dµ /dt=   g.dL/dt  soit dµ/dt=   gµ xB₀

Le mouvement de µ est écrit selon les trois axes, en utilisant les propriétés du produit vectoriel :
dµ_x/dt = g.(µ_yB₀z-µ_zB₀y) =  g.µ_yB₀       dµ_y/dt = g.(µ_zB₀x-µ_xB₀z) =   -g.µ_xB₀ et dµ_z/dt = g.(µ_xB₀y-µ_yB₀z) =  0. Il est facile de voir que µ décrit un mouvement circulaire uniforme, c'est à dire que   µ_x= acos(w₀t) et µ_y=asin(w₀t), avec une valeur de a donnée par

dµ_x/dt=-aw₀sin(w₀t) ou dµ_y/dt= -aw₀cos(w₀t) ce qui suppose que w₀=-g.B₀. Le mouvement est donc représenté par un vecteur w₀orienté en sens inverse de B₀.

Collections de moments dipolaires dans un champ magnétique

La Résonance magnétique est une spectroscopie peu sensible

Dans le cas d'une collection de spins, ils se distribuent de façon isotrope sur chaque tronc de cône, et ils sont tous soumis à un mouvement de rotation avec la vitesse angulaire w₀. De plus, l'existence du champ B₀ fait que les deux orientations n'ont pas la même énergie. En effet l'énergie d'interaction entre champ et dipôle est E= -µ.B₀où apparaît ici le produit scalaire: cette expression est équivalente à E=-µ_z.B₀ = - hgB₀/2p. m_I qui donne donc une valeur pour l'état fondamental

E_ef = -1/2.hgB₀/2ppour m_I=1/2 et E_ee=1/2.hgB₀/2p pour m_I=-1/2. Ces deux valeurs sont inférieures à l'énergie therm_Ique kT : par exemple, pour un proton dans un champ B₀= 10 Tesla, E_ef=-E_ee = -2,82.10^-25J (cf tableau) alors que kT=4,16.10^-21 J à 300K. Ceci signifie que les deux niveaux sont presque également peuplés à température ordinaire, selon une distribution de Boltzman :

N_ef/N= exp(-E_ef/kT)/[exp(-E_ef/kT)+exp(-E_ee/kT)]=1/[1+exp(2E_ef/kT)] dans lequel on pose E_ef/kT= e très petit. Il vient donc que

N_ef/N=1/(2+2e)=1/2.1/(1+e)=1/2.(1- e)= Bien entendu N_ee/N = 1-N_ef/N= 1/2.(1+e) et donc (N_ef-N_ee)/N = DN/N = - e = -E_ef/kT » 6.10^-5 . L'excès de l'état fondamental par rapport à l'état excité est donc de moins de 0,01%.  Il faut donc des concentrations importantes : de l'ordre de mM en RMN de ¹H et de l'ordre de µM en RPE.

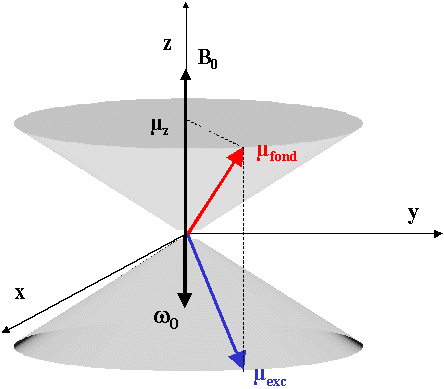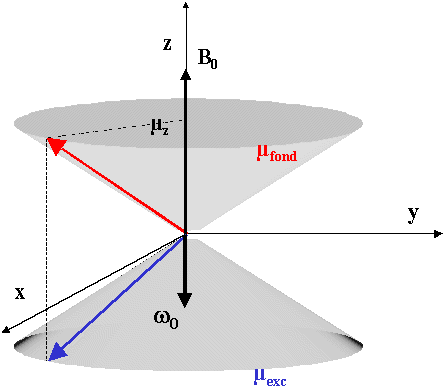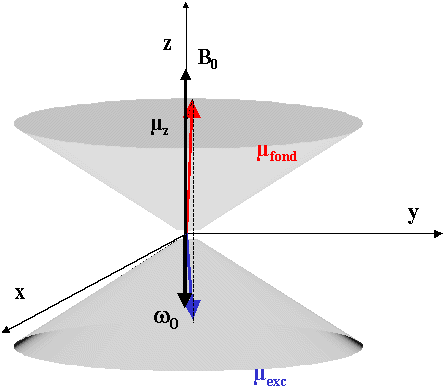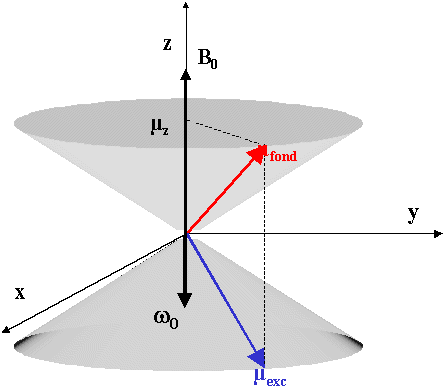
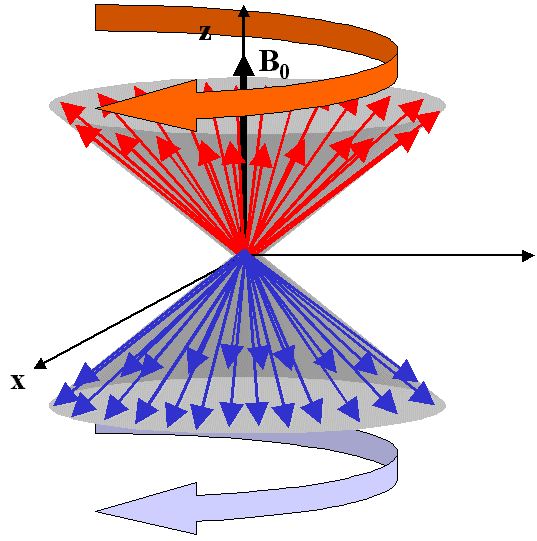
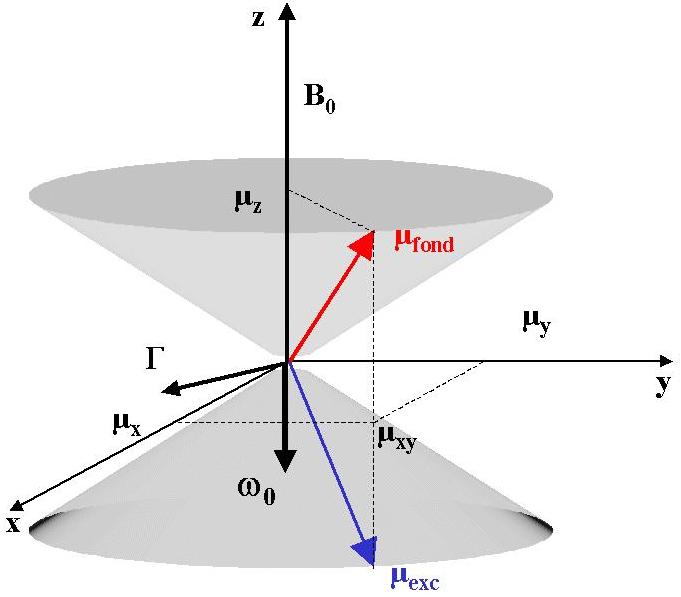
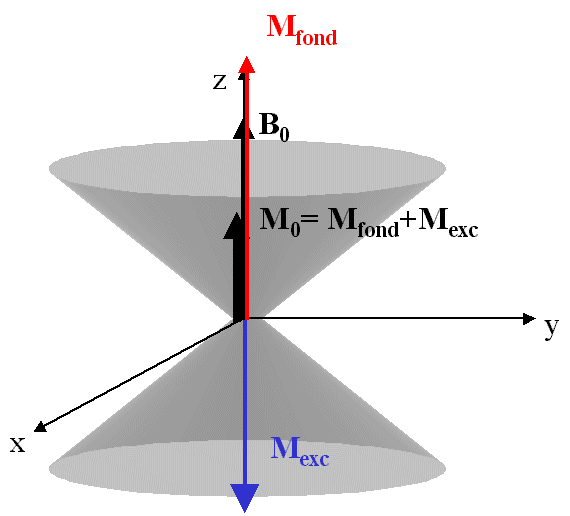
Il y a donc un très leger excès de spins sur le cône correspondant à l'état fondamental (rouges dans le dessin). Aux deux états, ils sont répartis de façon isotrope, et ils tournent dans le sens indiqué avec une vitesse angulaire w0. L'ensemble des spins à l'état fondamental se combinent en une aimantation  appelée Mfond, située sur l'axe et orientée comme B0.  De la même façon, l'ensemble des spins à l'état excité se combinent en une aimantation Mexc, oreintée en sens inverse et légèrement plus peite en module à Mfond. l'aimantation globale est donc M0, située sur l'axe z (les échelles ne sont pas respectées:  Mfond et Mexc sont beaucoup plus grandes que M0).

Spectroscopie de Résonance magnétique

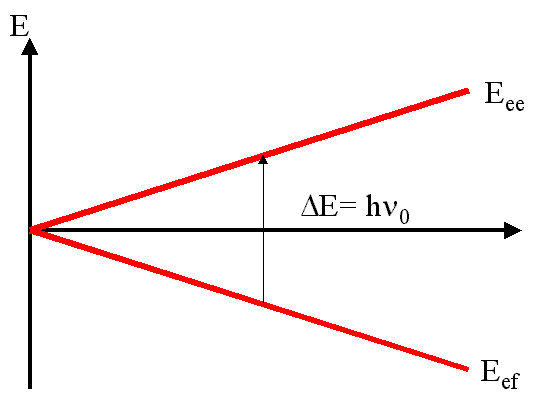
La transition entre l'état fondamental et l'état excité se fait à l'aide d'une radiation électromagnétique (sa partie magnétique en fait) dont la fréquence est donnée par hn0 = E_ee- E_ef =hgB₀/2psoit n₀ = w₀/2 = gB₀/2p. La fréquence qui provoque la transition est la même que celle de précession des moments dipolaires autour de B₀.
 

La fréquence est d'autant plus grande que B₀est plus grand.
On recherche un champ magnétique B₀le plus grand possible, pour que la différence de population entre les deux états soit la plus grande possible, mais aussi pour avoir une bonne résolution (voir plus loin). Les aimants utilisés sont alimentés par des bobines supra conductrices (refroidies à l'hélium liquide).

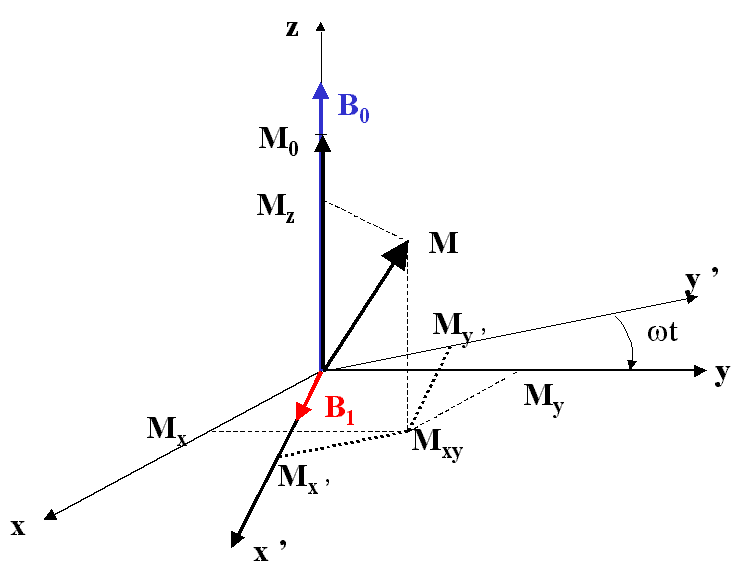
Pour que la fréquence n₀ réalise la transition entre les 2 niveaux, il existe une autre condition: il faut que le champ magnétique correspondant (appelé B₁) tourne dans le plan xOy avec une vitesse angulaire proche de w_0<(sinon égale). L'effet de ce champ sera de faire tourner l'aimantation de M₀ à M (cf plus loin) de telle façon qu'aaparaissent des composantes de M dans le plan x0y (M_x et M_y). Pour la facilité du calcul, on attache à B₁un axe Ox', tournant avec lui avec une vitesse angulaire w. On utilisera plus loin les composantes de M sur les 3 axes du référentiel tournant : M_z' (identique à M_z), M_x' et M_y'.

 

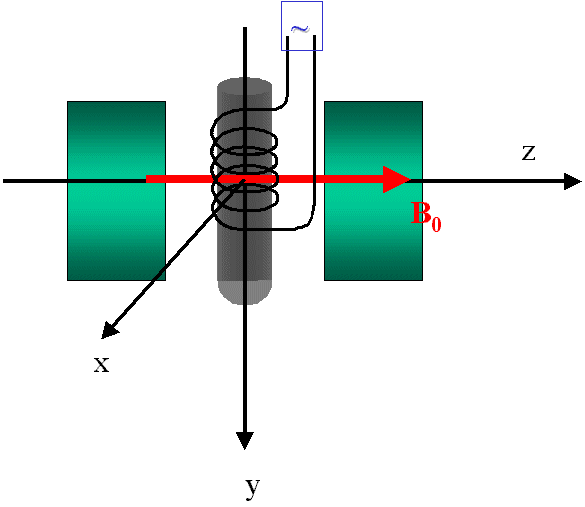
Pour réaliser ce champ tournant on opère matériellement de la façon suivante : Le champ magnétique B₀ fournit par l'aimant définit l'axe Oz. L'échantillon est sité le long de l'axe appelé y. Une bobine entourant l'échantillon est alimentée en courant de haute fréquence (de l'ordre de n₀). Il s'y crée donc un champ magnétique longitudinal, le long de y, oscillant avec la même fréquence.

 

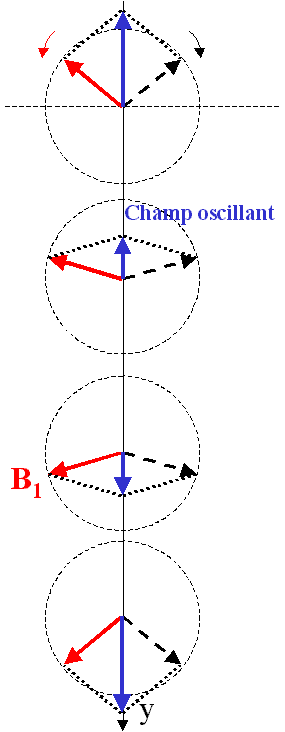
On peut représenter ce champ oscillant comme la somme de 2 champs, égaux en amplitude, tournant en sens inverse l'un de l'autre. Seul le champ B1, tournant dans le bon sens, affecte les spins, et sera donc considéré dans la suite. En effet, il est facile de voir que l'autre champ tourne à vitesse angulaire 2 w dans le repaire tournant. Ce dernier n'étant pas en phase avec l'aimantation, il ne joue aucun rôle dans la suite des événements.

Equations de Bloch

La variation de l'aimantation sous l'effet de B₀ et B₁s'écrit comme pour ce que l'on a déjà vu avec les moments dipolaires :

dM/dt = gMx(B₀ + B₁)

Mais cette expression est plus facile à calculer en tenant compte de l'expression de (dM/dt)_{repère mobile} qui découle de l'expression classique du changement de référentiel suivant :

(dM/dt)_{repère fixe}= (dM/dt)_{repère mobile}+ wxMoù w est un vecteur représentant la rotation de B₁, orienté le long de Oz, de module w.
On peut réécrire cette expression sous la forme (dM/dt)_{repère mobile}= (dM/dt)_{repère fixe}+ Mxw  ce qui conduit à  l'expression suivante :
(dM/dt)_{repère mobile}=gMx(B₀ + B₁+ w/g). Il suffit alors d'exprimer les trois produits vectoriels dans les trois directions du repère tournant pour obtenir les expressions suivantes, en remarquant que w₀= - g.B₀sur l'axe Oz (voir plus haut). Elles contiennent un terme supplémentaire qui tient compte de la relaxation de tout système écarté de l'équilibre thermodynamique (voir ci-dessus). On suppose que cet effet diminue M_x'et M_y' (jusqu'à atteindre leur valeur nulle à l'équilibre) selon une loi d'ordre 1, avec une constante de temps appelée T₂. De la même façon, M_z augmente jusqu'à sa valeur M₀à l'équilibre, selon une loi de même type, proportionnelle à la différence M₀-M_z, avec une constante de temps T₁. La signification de T₁ et T₂ est expliquée plus loin.

(dM/dt)_x'=g(M_y'.B_0z - M_z.B_0y' + M_y'.B_1z- M_z.B_1y') + M_y'.w_z- M_z.w_y' - M_y'/T₂= M_y' (w-w₀) - M_x'/T₂  = 0

(dM/dt)_y'=g(M_z.B_0x' - M_x'.B_0z + M_z.B_1x'- M_x'.B_1z ) + M_z.w_x'- M_x'.w_z  - M_y'/T₂= -M_x' (w-w₀) + g.M_z.B₁ - M_y'/T₂ = 0
(dM/dt)_z'=g(M_x'.B_0y' - M_y'.B_0x' + M_x'.B_1y'- M_y'.B_1x') + M_x'.w_y'- M_y'.w_x' +  (M₀-M_z)/T₂= - g.M_y' B₁ + (M₀-M_z)/T₁ = 0

Une simplification supplémentaire peut être appliquée dans le cas où on fait une spectroscopie classique. En effet, le spectre revient à observer le signal qui varie à la suite d'un balayage en fréquence w. Si ce balayage est lent, l'état quasi stationnaire est toujours réalisé (d'où les 3 "=0" au bout de chaque équation). Les trois équations différentielles ci-dessus se transforment donc en 3 équations linéaires à 3 inconnues, faciles à résoudre .

On en déduit facilement les expressions suivantes avec des dénominateurs communs (D) :
M_x' = gB₁T₂²M₀(w-w₀) /D
M_y' = gB₁T₂M₀ /D
M_z = M₀ - g²B₁²T₁T₂M₀/D
Pour lesquels D = 1 + g²B₁²T₁T₂+T₂² (w-w₀)²
La valeur de M_y' représente le spectre classique (dit en absorption), avec une raie centrée à w₀,dont la forme mathématique caractéristique a/(b +c Dw²) est appelée Lorentzienne. Cette forme est décrite en détail dans le chapitre consacré à la spectroscopie d'impulsion actuellement pratiquée (impulsion, FID et transformée de Fourier) au lieu du spectre obtenu par balayage, quasi complètement abandonné à ce jour.